TL;DR
Our Web version, AniTop-Web, is now live! Check it out to simulate and visualize integrable tops in your browser!
Studied Lagrangian and Hamiltonian Mechanics applied to the modeling of three integrable top formulations: Euler, Lagrange, and Kovalevskaya tpos. Led a team effort that models of top motion, from PDE solutions to in homogeneous transformations. Architected a modular Integrable Tops simulator and animation package, available in MATLAB and Web. I learned a great deal of not only practical modeling of physical dynamical systems through Lagrangian and Hamiltonian Mechanics, solving numerical sim-real gap problems, but also a great deal of teamwork, effective communication, and project planning.
Deliverables
- Download the Project Report here
- Download the Project Poster here
- See our AniTop MATLAB Package here
- The AniTop Python Package featuring GPU-accelerated real-time rendering is in the works! Check back later for more info!
About the AniTop Project
Both curious about modeling of freely spinning tops with complex energy states, the efficient computer simulation of these motion, and the research process in mathematics in general, I applied to participate in Dr. Alejandro Bravo-Doddoli's Lab of Geometry section as a software specialist, and work with three other talented undergraduate students to create an efficient numerical simulation of three integrable tops, and render them as animated videos to provide researchers an intuitive visualization of spinning tops under various initial conditions. This project features the modeling and animation parts of three integrable tops: Euler, Lagrange, and Kovalevskaya tops.
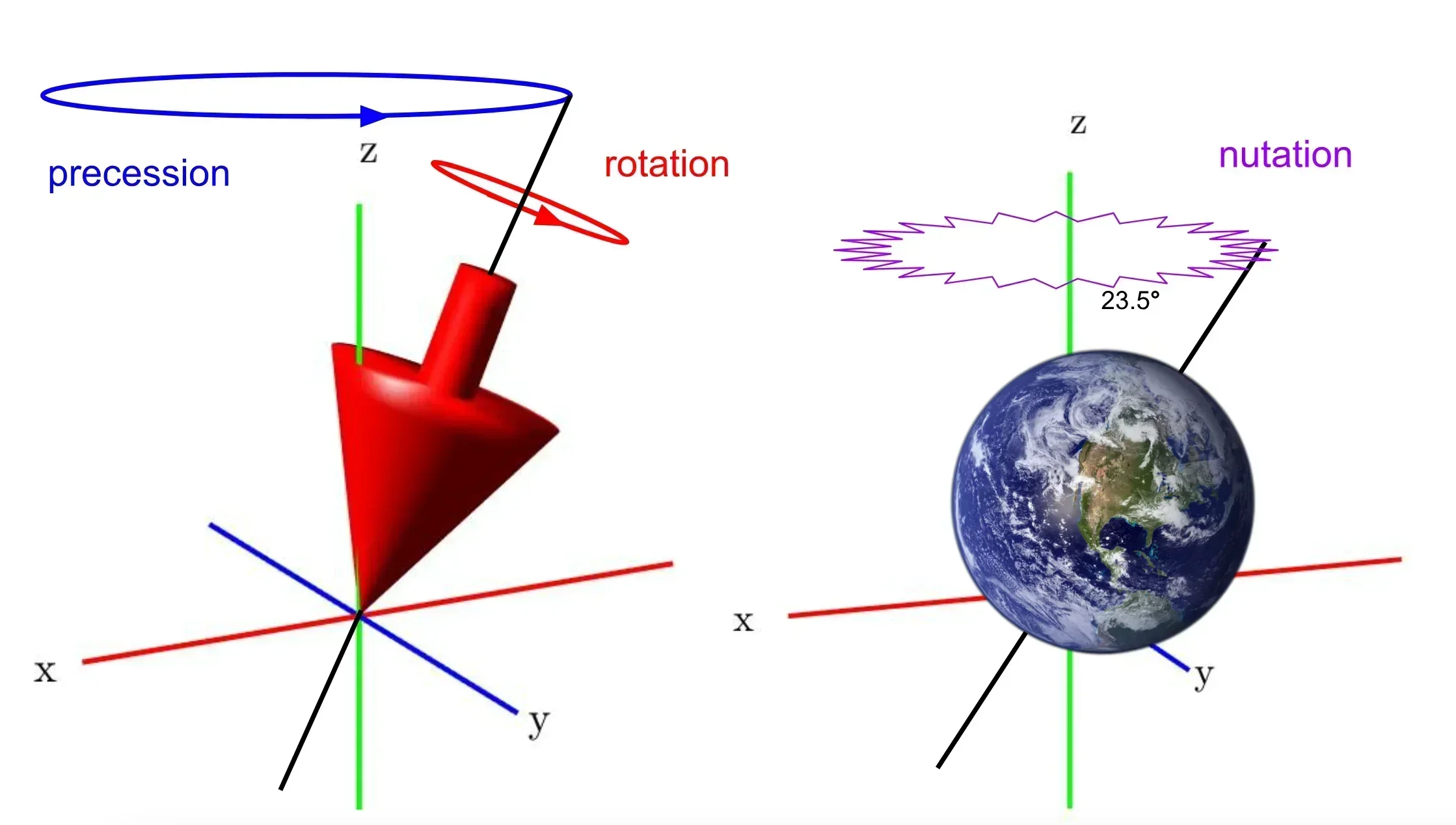
This semester-long project began with a background introduction, where Prof. Doddoli introduced our team to the concept of Lagrangian Mechaincs and Hamiltonian Mechanics, a way of modeling motion through energy states, rather than the Newtonian Mechanics, through Forces.
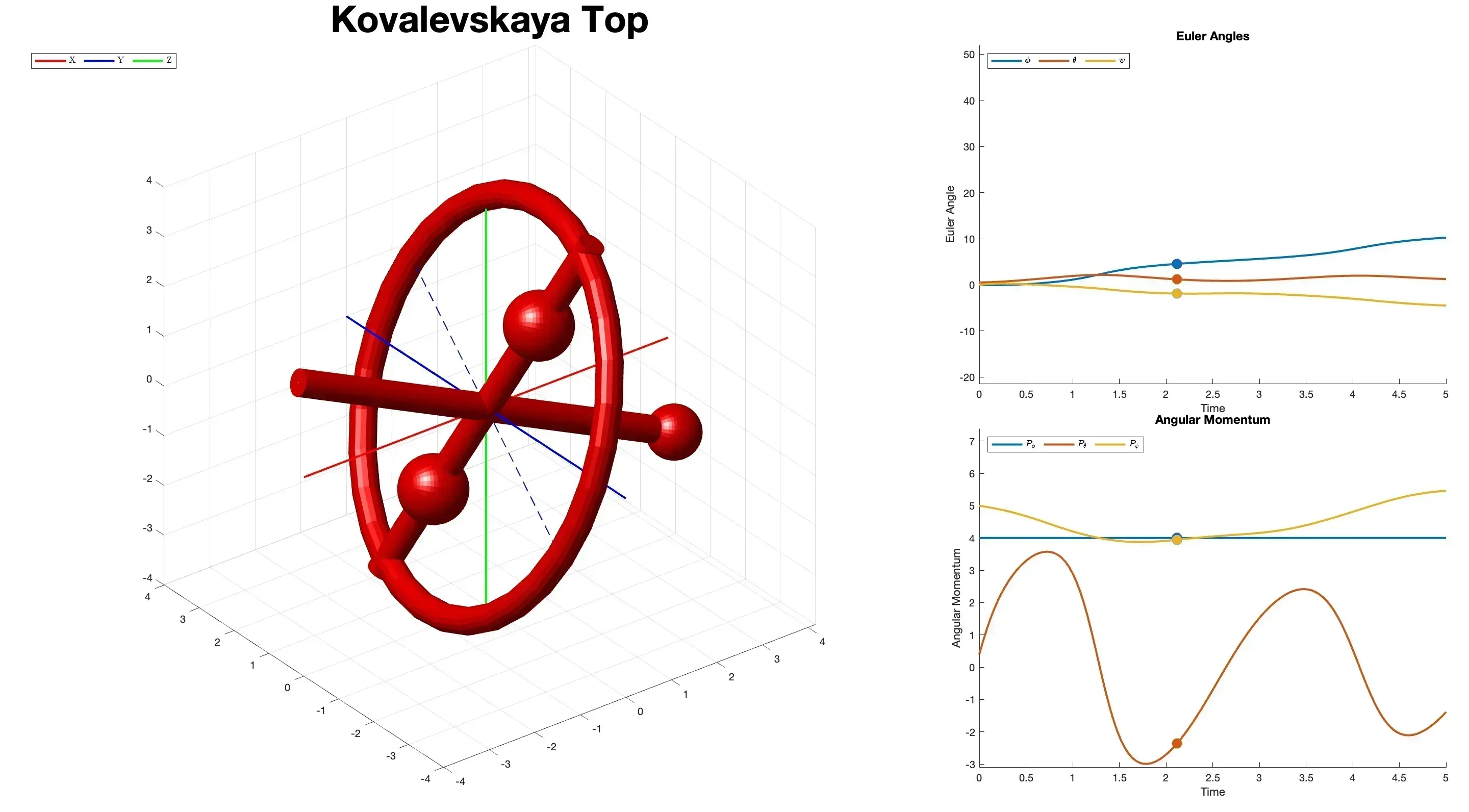
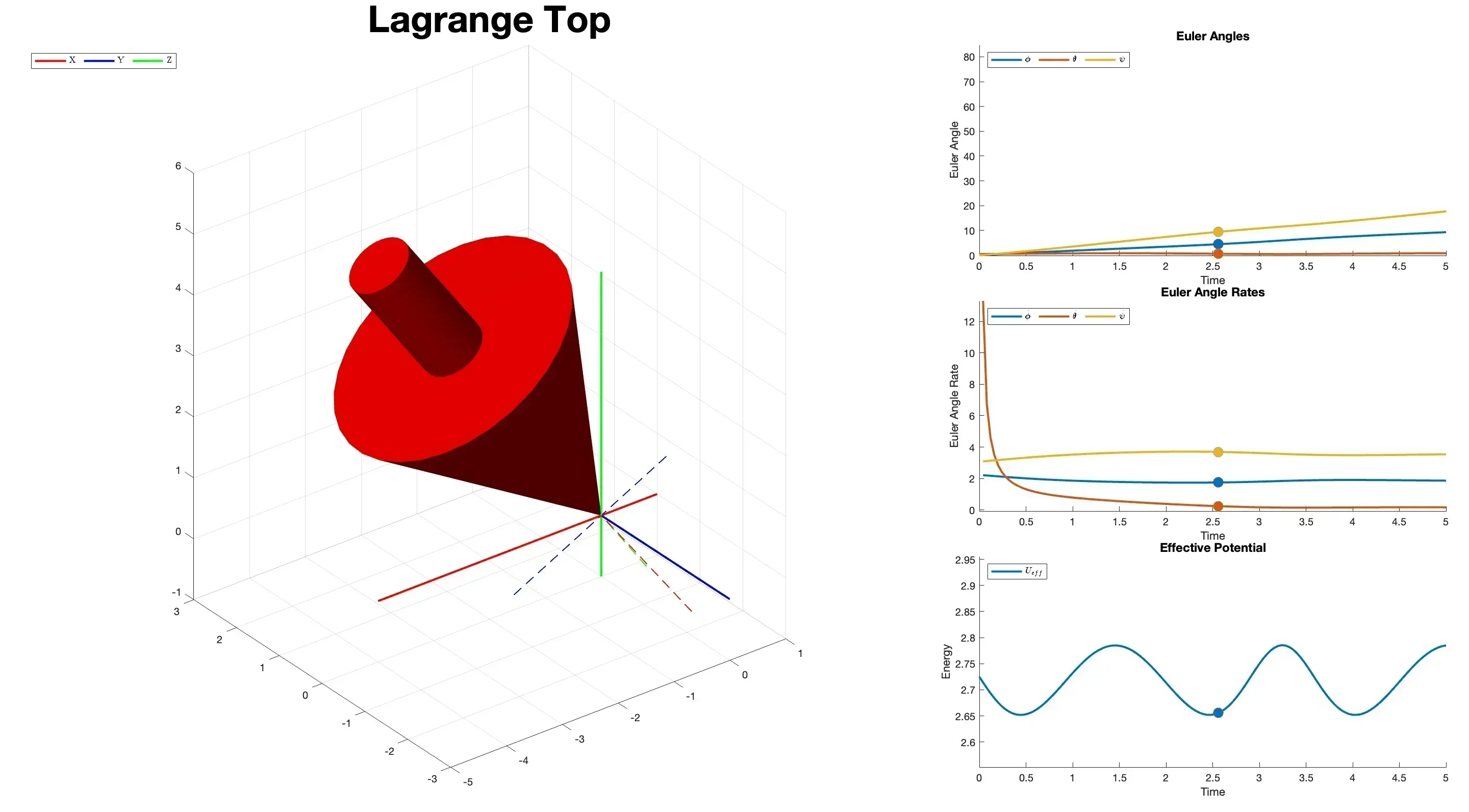
As an outcome of this project, we release an open source beta version of the AniTop (short for Animating Tops) package for MATLAB. Written in pure MATLAB, this package includes functions for numerically simulating the motion of three Integrable tops, given their valid initial conditions, and then produce a 20-second video that renderes that motion with respect to the world axis. The AniTop MATLAB package is available for free on Github, and a GPU-accelerated AniTop Python package is in the making.
What I gained
Teamwork with Diverse Background
Joining the team originally as the software specialist, I learned much about team coordination in a team with diverse expertise and background. I gained invaluable experience in both receiving and delivering technical content and background to an otherwise amateur group of colleagues.
Sub-Tasks Mechanism To maximally leverage our diverse backgrounds, we designed our project work as sub-tasks, and assign sub-tasks to subset of individuals. Each member may be on more than one sub-tasks, where their knowledge is invaluable. While everyone participates in the meetings of each sub-task, concrete work and discussion inputs are expected for those on the sub-task. This structure also enabled us to track the progress of each problem currently solving, create a new sub-task every time a new problem is encountered, and make sure every problem is clearly communicated with the Professor for his input.
Rooted from practices in larger research labs (and from the git-issue mechanism), our sub-task procedure works surprisingly well throughout the semester. Our subteams closely work with each other during and after meetings, thanks to people working on various sub-tasks at once. The sub-teams deliver solutions and discussion questions on various problems in understanding equations, implementing numerical differential equations, as well as code structuring and contribution. The completion of each of the sub-tasks provide a concrete step towards the success of this research task, and we are able to deliver a fully working product to the Professor's research group, where this intuitive tool is helping them gain more intuitive understanding of the bifurcation theory studied in top dynamics.
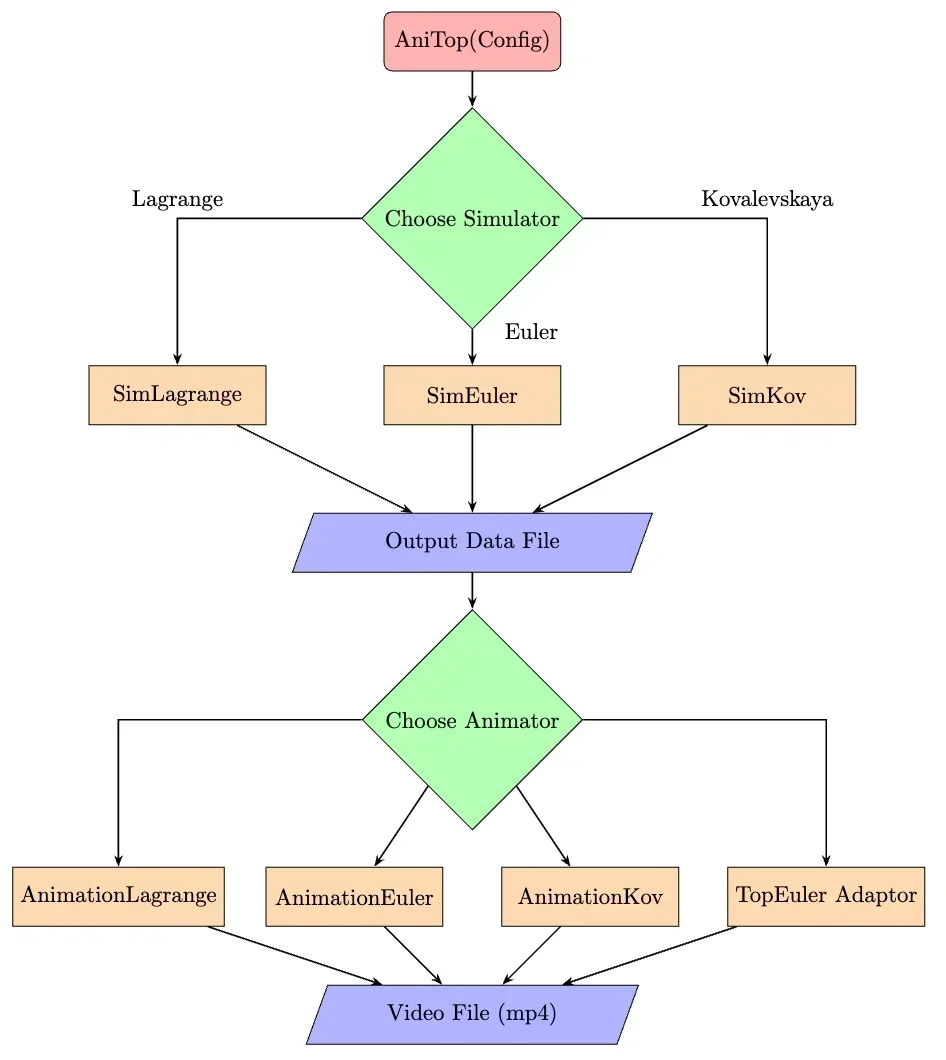
Concise Communication During this process, I practised consciously removing jargons in my communications with my teammates and with the professor. To deliver the software architecture I designed to my teammates, I made a flowchart and explained each part from big-picture to details. While not familiar with programming in general, especially with GUI programming, my teammates are able to quickly grasp the two ends of the spectrum: backend computation and frontend display. Further, I implemented a toy example of what would become a parent-children class structure for the Animators (classes that handle animation of the Tops motion, including initializing a window, setting the correct shape of mesh to display, as well as updating each step), my teammates were able to follow up and propose that they can individually work on sub-classes that generate meshes for individual tops, while I work on the base class that involves more technical designs. With this mechanism, we pieced together a set of animation classes that work seamlessly with each other with just a few hours of tuning and debugging.
Mechanics with Energy
While interested in robotics, I was primarily studying the intelligence part, leaving my understanding of modern mechanics modest at best. It has been a surprise for me to gain practical experience with Lagrangian and Hamiltonian mechanics, the foundation of complex dynamics modeling. I participated in a divide-and-conquer effort in deriving the energy state differential equations with respect to each of the rotating axes. For this task, we formed two sub-tasks in parallel, trying to derive the differential equations in two groups of two each, before comparing solutions and what is documented in literature. Four iterations of this process allowed us to line-up our derivation with the literature. During the process, we gained deeper understanding of the symbols and notations in the literature, as well as the reasons for making those choices, so that we are not blindly copying equations while implementing the simulators, but understanding what we do.
While still a novice in understanding Mechanics modeling through energy, I appreciate the opportunity to gain exposure to those topics. This opportunity also helped me better understand the details of the FastANT project at the BIRDS Lab, and enable me to conduct analysis and build model-based simulation to explain the behaviors of event-select systems in multi-legged robot motion modeling.
Handling Orientation
While I was aware that Euler angles in rotation suffer from singularities, and thus numerical instabilities in numerical simulations, this project gives my team and I a concrete opportunity to solve ths problem in a real product we are trying to deliver. Upon observing the spikes in our simulated Euler Angles, caused by infinitesimally small floating point numbers, we designated a special task group to resolve this issue numerically.
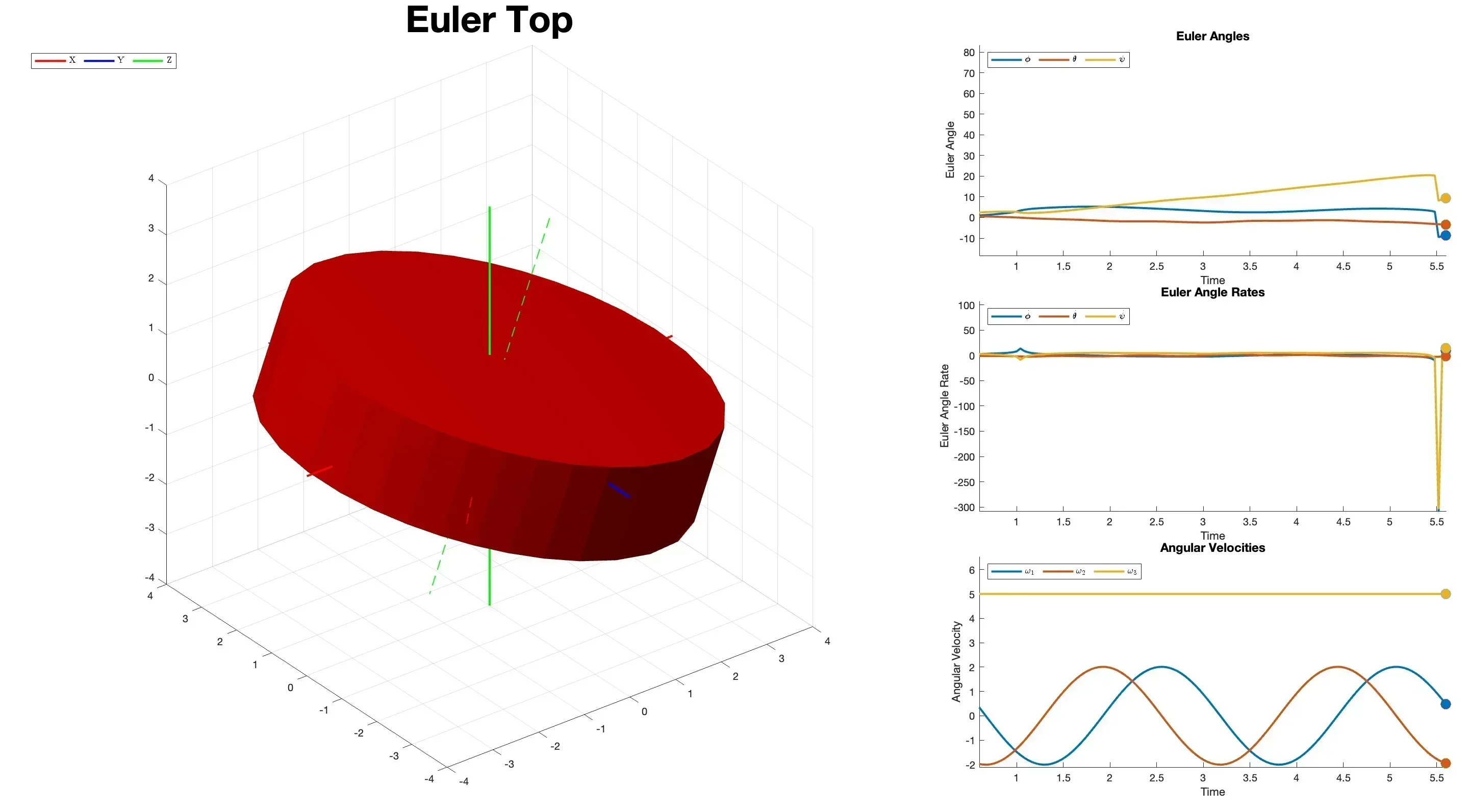
While the task was never completed during that semester, due to the challenges of deriving equations with quaternions, we set a concrete step towards that direction by providing postprocessing on the integrated results. Our journey never ended there though. During the development of the AniTop Python package, two of us are still working on expressing the equations in terms of Quaternion rotation to fully resolve the numerical instability in the current MATLAB package.
Closing Remarks
Overall, I was time and time again proud that something unexpected came up to me and I caught that as well as I could. The more projects I participate in, the more I realize that the more I know, the more I don't know. This project is a perfect ilustration of that motto. I am never sorry that I don't knw more. The knowledge in this work is simply too much for one ordinary man to learn during their lifetimes, leave alone in 20 years. Yet, on my journey towards the state of the art, I am proud that I kept my mind open to new opportunities, new ideas, and new fields that I would otherwise never get to learn about.
Steve Jobs once said that what you do now may not be obvious for your future, but it will piece together many years in the future, and you would be glad that you had done what you had done. Indeed, I aim to carry my expanding horizon into my future research, innovatively solve problems through cross-field knowledge and collaboration, and hopefully make contributions to the knowledge, and of course, well being, of mankind.